CS 1510 Midterm 2

Fall 2000

1.

(20 points)

(a)

Explain how to compute the minimum of n numbers 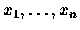$x_1, \ldots, x_n$ in O(1) time with n² processors on a common CRCW PRAM.

(b)

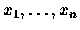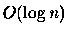Explain how to compute the minimum of n numbers $x_1, \ldots, x_n$ in $O(\log n)$ time with n processors on a EREW PRAM. That is you want $T(n, p=n) = O(\log n)$.

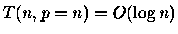(c)

You have a parallel algorithm A with the property that doubling the number of processors cuts A's running time by half. What does this say about the efficiency of A? Start your answer with a definition of efficiency.

(d)

State the folding principle.

2.

(20 points) Show that the Hamiltonian Cycle problem is self-reducible. The decision problem is to take a graph G and decide if G contains a Hamiltonian cycle. The optimization problem must also return the actual Hamiltonian cycle if one exists. So you must show that if the decision problem has a polynomial time algorithm then the optimization problem also has a polynomial time algorithm. Recall that a Hamiltonian cycle is a cycle that visits every vertex exactly once.

3.

(20 points) Consider the following problem:

INPUT: Strings $P = P_1, \ldots, P_m$ and $T = T_1, \ldots, T_n$

OUTPUT: 1 if P is a substring of T, and 0 otherwise.

Note that P is a substring of T if there exist an integer i, $1 \le k \le n - m +1$, such that for all k, $1 \le k \le m$, it is the case that P_k = T_i+k-1, that is, P₁ = T_i, and P₂ = T_i+1, and P₃ = T_i+2, and ... and P_m = T_i+m-1. So if P=abac and T=abbbbabacccc, then one can verify that P is substring of T by taking i=6.

Give an EREW algorithm for this problem whose running time is $O(\log n)$ using at most n² m² processors.

4.

(20 points) Consider the following UNDIRECTED DOMINATING SET problem:

INPUT: An undirected graph G and an integer k.

OUTPUT: 1 if G has a dominating set of size k or less. A dominating set is a collection S of vertices with the property that every vertex v in G is either in S, or there is an edge between a vertex in S and v.

Show that this problem is NP-hard. Use the fact that the following VERTEX COVER problem in NP-complete:

INPUT: An undirected graph H and an integer $\ell$.

OUTPUT: 1 if H has a vertex cover of size $\ell$ or less. Recall that a vertex cover a collection S of vertices with the property that every edge in H is incident on a vertex in S.

Some partial credit will be awarded if you set up the reduction correctly.

5.

(20 points) You are given a collection of n VLSI chips. Up to 2n/3 of the chips may not be reliable. There is jig that allows you to test pairs of chips. Say you are testing a pair X and Y of chips. If X is good then X will accurately report on whether Y is good or not. If X is bad, X may say that Y is good, or X may say that Y is bad (independent of whether Y is good or bad). If Y is good then Y will accurately report on whether X is good or not. If Y is bad, Y may say that X is good, or Y may say that X is bad (independent of whether X is good or bad). You have no other way of determining whether a chip is good or bad. Show that it is not possible to identify a good chip with surety under this setting.

Note that I am looking for a concrete convincing argument here -- not a wishy-washy ``I don't see how you could do it.'' argument.

6.

(20 points) Consider the following problem. The input consists of a sequence $R = R_0, \ldots, R_n$ of non-negative integers, and an integer k. The number R_i represents the number of users requesting some particular piece of information at time i ( say from a data-base server, a name server, a www server, etc). If the server broadcasts this information at some time t, the the requests of all the users who requested the information strictly before time t are satisfied. The server can broadcast this information at most k times. The goal is to pick the k times to broadcast in order to minimize the total time (over all requests) that requests/users have to wait in order to have their requests satisfied.

As an example, assume that the input was R = 3, 4, 0, 5, 2, 7 (so n=6) and k=3. Then one possible solution (there is no claim that this is the optimal solution) would be to broadcast at times 2, 4, and 7 (note that it is obvious that in every optimal schedule that there is a broadcast at time n+1 if $R_n \ne 0$). The 3 requests at time 1 would then have to wait 1 time unit. The 4 requests at time 2 would then have to wait 2 time units. The 5 requests at time 4 would then have to wait 3 time units. The 2 requests at time 5 would then have to wait 2 time units. The 7 requests at time 6 would then have to wait 1 time units. Thus the total waiting time for this solution would be

3 * 1 + 4 * 2 + 5*3 +2*2 + 7*1