CS 1510 Final Exam

Summer 1998

1.

(40 points) Consider the following problem. The input consists of the lengths $\ell_1, \ldots, \ell_n$, and access probabilities $p_1, \ldots, p_n$, for n files $F_1, \ldots, F_n$. The problem is to order these files on a tape so as to minimize the expected access time. If the files are placed in the order $F_{s(1)}, \ldots, F_{s(n)}$ then the expected access time is

$$\sum_{i=1}^n p_{s(i)} \sum_{j=1}^{s(i)} \ell_{s(j)}$$

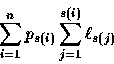
Don't let this formula throw you. The term $p_{s(i)} \sum_{j=1}^{s(i)} \ell_{s(j)}$ is the probability that you access the ith file times the length of the first i files.

For each of the below algorithms, either give a proof that the algorithm is correct, or a proof that the algorithm is incorrect.

(a)

Order the files from shortest to longest on the tape. That is, 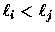$\ell_i < \ell_j$ implies that s(i) < s(j).

(b)

Order the files from most likely to be accessed to least likely to be accessed. That is, p_i < p_j implies that s(i) > s(j).

(c)

Order the the files from smallest ratio of length over access probability to largest ratio of length over access probability. That is, 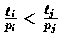$\frac{\ell_i}{p_i} < \frac{\ell_j}{p_j}$ implies that s(i) < s(j).

2.

(20 points) Give an algorithm for the following problem whose running time is polynomial in n + L + k. Input: Positive integers $v_1, \ldots, v_n$, k, and L. Output: A solution (if one exists) to $(\sum_{i=1}^n x_i v_i) = L$ where each x_i is an integer satisfying $1 \le x_i \le k$.

3.

(20 points) Give a polynomial time algorithm that takes three strings, A, B and C, as input, and returns the longest sequence S that is a subsequence of A, B, and C.

4.

(20 points) Show that the following problem is NP-hard: INPUT: A graph G. Let n be the number of vertices in G. OUTPUT: 1 if G contains a simple cycle with n-1 edges, and 0 otherwise. Use the fact the the following problem is NP-hard: INPUT: A graph G. OUTPUT: 1 if G contains a simple cycle that spans G, and 0 otherwise. Note that a cycle is simple if it doesn't visit any vertex more than once. A cycle spans G if every vertex is included in the cycle.

5.

(20 points) Show that the Vertex Cover Problem is self-reducible. The decision problem is to take a graph G and an integer k and decide if G has a vertex cover of size k or not. The optimization problem takes a graph G, and returns a smallest vertex cover in G. So you must show that if the decision problem has a polynomial time algorithm then the optimization problem also has a polynomial time algorithm. Recall that a vertex cover is a collection S of vertices with the property that every edge is incident to a vertex in S.

6.

(20 points) Give an algorithm that given an integer n computes n!, that is n factorial, in time $O(\log n)$ on an EREW PRAM with n processors. Make the unrealistic assumption that a word of memory can store arbitrarily large integers.

7.

(20 points) Give an algorithm for the minimum edit distance problem that runs in poly-log time on a CREW PRAM with with a polynomial number of processors. Here poly-log means $O(\log^k n)$ where n is the input size, and k is some constant independent of the input size.

Recall that the input to this problem is a pair of strings $A=a_1 \ldots a_m$ and $B=b_1 \ldots b_n$. The goal is to convert A into B as cheaply as possible. The rules are as follows. For a cost of 3 you can delete any letter. For a cost of 4 you can insert a letter in any position. For a cost of 5 you can replace any letter by any other letter.