CS 1510 Midterm 1

Fall 1998

1.

(40 points) You wish to drive from point A to point B along a highway minimizing the time that you are stopped for gas. You are told beforehand the capacity C of you gas tank in liters, your rate F of fuel consumption in liters/kilometer, the rate r in liters/minute at which you can fill your tank at a gas station, and the locations $A=x_1, \ldots, B=x_n$ of the gas stations along the highway. So if you stop to fill your tank from 2 liters to 8 liters, you would have to stop for 6/r minutes. Consider the following two algorithms:

(a)

Stop at every gas station, and fill the tank with just enough gas to make it to the next gas station.

(b)

Stop if and only if you don't have enough gas to make it to the next gas station, and if you stop, fill the tank up all the way.

For each algorithm either prove or disprove that this algorithm correctly solves the problem.

2.

(20 points) The binomial coefficient $n \choose k$ can be defined recursively in the following way: ${n \choose k}=1$ if k=0, or k=n, else

$${n \choose k} = {n -1 \choose k-1} + {n-1 \choose k}$$

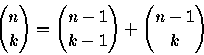
(a)

Write a recursive C function Binomial to compute $n \choose k$.

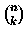(b)

Show that the number of nodes in the recursive call tree for the Binomial function can be exponential in n and k.

(c)

What is maximum number of distinct subproblems in the recursive call tree as a function of n and k?

(d)

Write iterative array based code to compute 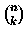$n \choose k$ that would run in time polynomial in n and k.

3.

(20 points) The input to this problem consists of:

• gems $G_1, \ldots, G_n$,

• a positive integer value v_i in dollars for each G_i,

• a positive integer weight w_i in kilograms for each G_i,

• a type T_i, either ruby, diamond or emerald, for each G_i,

• and integers V, R, E, D.

The problem is to find the minimum weight subcollection of gems with

• total value at least V,

• exactly R rubies,

• exactly E emeralds, and

• exactly D diamonds.

Given an algorithm for this problem that runs in time polynomial in n+L, where $L = \sum_{i=1}^n v_i$.

4.

(20 points) Consider the problem where the input is a collection of n train trips within Germany. For the ith trip T_i you are given the date d_i of that trip, and the non-discounted fare f_i for that trip. The German railway system sells a Bahncard for 240 Marks that entitles you to a 50% fare reduction on all train travel within Germany within 1 year of purchase. The problem is to determine when to buy a Bahncard to minimize the total cost of your travel. For example if the input was d₁ = January 11, 1997, f₁=20 Marks, d₂ = February 11, 1998, f₂=200 Marks, d₃ = January 11, 1999, f₃=200 Marks, d₄ = March 13, 1999, f₄=100 Marks, d₅ = February 11, 2002, f₅=200 Marks, and d₆ = January 11, 2003, f₆=600 Marks, then you might buy a Bahncard on February 11, 1998, and February 11, 2002, resulting in a total cost of 1200 Marks. Give a polynomial time algorithm for this problem. The running time of you algorithm should be independent of the cost of a Bahncard.