- 1.
- The input to this problem consists of an ordered list of n words.
The length of the ith word is wi, that is the ith
word takes up wi spaces. (For simplicity assume that
there are no spaces between words.) The goal is to
break this ordered list of words into lines, this is called
a layout.
Note that you can not reorder the words.
The length of a line is the sum of the
lengths of the words on that line.
The ideal line length is L.
No line may
be longer than L, although it may be shorter.
The penalty for having a line of length K is
L-K.
The total penalty is the sum of the line penalties.
The problem is to find a layout that
minimizes the total penalty.
Prove of disprove that the following greedy algorithm correctly
solves this problem.
For i= 1 to n
Place the ith word on the current line if it fits
else place the ith word on a new line
- 2.
- The input to this problem consists of an ordered list of n words.
The length of the ith word is wi, that is the ith
word takes up wi spaces. (For simplicity assume that
there are no spaces between words.) The goal is to
break this ordered list of words into lines, this is called
a layout.
Note that you can not reorder the words.
The length of a line is the sum of the
lengths of the words on that line.
The ideal line length is L.
No line may
be longer than L, although it may be shorter.
The penalty for having a line of length K is
L-K.
The total penalty is the maximum of the line penalties.
The problem is to find a layout that
minimizes the total penalty.
Prove of disprove that the following greedy algorithm correctly
solves this problem.
For i= 1 to n
Place the ith word on the current line if it fits
else place the ith word on a new line
- 3.
- Consider the Chained Matrix Multiplication Problem from the
text. The input to this problem is
a sequence of n matrices
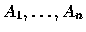 .
The output is parenthesization of
the
product
.
The output is parenthesization of
the
product
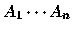 that
results in the fewest number of scalar multiplications.
We assume that the naive matrix multiplication algorithm
is used to multiply pairs of matrices. This naive algorithm
uses abc scalar multiplications to multiply an
a by b matrix by an b by c matrix.
Let MIN(i, j),
that
results in the fewest number of scalar multiplications.
We assume that the naive matrix multiplication algorithm
is used to multiply pairs of matrices. This naive algorithm
uses abc scalar multiplications to multiply an
a by b matrix by an b by c matrix.
Let MIN(i, j),
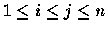 be the minimum
number of scalar multiplications required to compute the product
be the minimum
number of scalar multiplications required to compute the product
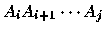 .
.
- (a)
- Explain how the feasible solutions to an instance of this problem can
be viewed as trees.
- (b)
- Give a recurrence relation for MIN(i,j).
- (c)
- Use this relation to compute the remaining entry in the
following table when
where A1 is a 13 by 5 matrix,
A2 is a 5 by 89 matrix,
A3 is a 89 by 3 matrix, and
A4 is a 3 by 34 matrix.
Show your calculations.
| |
j=1 |
j=2 |
j=3 |
j=4 |
| i=1 |
0 |
5785 |
1530 |
|
| i=2 |
UNDEFINED |
0 |
1535 |
1845 |
| i=3 |
UNDEFINED |
UNDEFINED |
0 |
9078 |
| i=4 |
UNDEFINED |
UNDEFINED |
UNDEFINED |
0 |
- (d)
- In the above example, which matrix
multiplication should be performed last in order to
minimize the number of scalar multiplications? Justify your
answer.
- 4.
- The input to this problem consists of:
- Gems
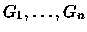 ,
,
- with an integer value vi in dollars for each Gi, and
- with a type, ruby or diamond, for each gem.
The problem is to determine if it is possible
to partition of the gems into two collections P and Q such that
- the number of rubies in P is
greater than the number of rubies in Q,
- the number of diamonds
in P is less than the number of diamonds in Q.
- The expression
is maximized.
Note that a partition means that every gem must be in exactly one of
P or Q. Given an algorithm for this problem that runs in time
polynomial in n+L,
where
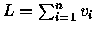 .
.
- 5.
- The input to this problem is a pair of strings
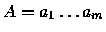 and
and
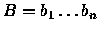 .
The goal is to convert A into B as cheaply
as possible. The edit rules are as follows.
For a cost of 4 you can delete any letter.
For a cost of 5 you can insert a letter in any position.
For a cost of 6 you can replace any letter by any other letter.
For a cost of 66 you can delete any suffix of A.
So the output should be a sequence of edits that convertes
A to B as cheaply as possible. Give a polynomial time
algorithm for this problem.
.
The goal is to convert A into B as cheaply
as possible. The edit rules are as follows.
For a cost of 4 you can delete any letter.
For a cost of 5 you can insert a letter in any position.
For a cost of 6 you can replace any letter by any other letter.
For a cost of 66 you can delete any suffix of A.
So the output should be a sequence of edits that convertes
A to B as cheaply as possible. Give a polynomial time
algorithm for this problem.
For example, you can convert A=abcabc to B=aba via
the following sequence:
abcabc at a cost of 66 can be converted to
abc, which at cost of 6 can be converted to
abc.
Thus the total cost for this conversion would be 72.
This conversion is not optimal.
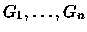 ,
,
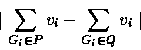
![]() .
.