CS 1510 Midterm 1

Fall 2002

1.

(40 points) Consider the following real-world budget problem that challenges your instructor, and many other government/academic bureaucrats. The input consists of a collection of accounts $A_1, \ldots, A_n$, and a collection of events $E_1, \ldots, E_m$. Each account A_i has a start date r_i and an end date d_i. Further each account A_i contains an amount a_i of money. Each event E_j happens on a date e_j and has a cost of c_j dollars. The cost c_j for event E_j, or some portion thereof, can be charged to any account A_i that is open during the date e_j, that is, any account A_i where $r_i \le e_j \le d_i$. Note that an event can be paid for by more one account; For example an event of cost $3 can be paid by $1 from one account and $2 from another account. Obviously, the account A_i can not contribute more than a_i dollars towards paying for events. The problem is to determine which costs should be charged to which accounts. The goal is to find an algorithm that will find a feasible method of paying for the costs of the events, if it is possible to do so.

We consider greedy algorithms for this problem that pay for the events by non-decreasing order of date. For simplicity assume that the events are ordered by date, that is, $e_1 \le e_2 \le \ldots \le e_m$. So our greedy algorithms first determine how to pay for event E₁, then determine how to pay for event E₂, then determine how to pay for event E₃, etc. Note that we are often forced to use such a greedy algorithm in practice because we are not aware of events until they happen. The algorithms differ in how they pick the accounts to pay for the current event. Consider the following two algorithms, Early and Level:

Early

Assume that events 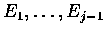$E_1, \ldots, E_{j-1}$ have been paid for, and we now wish to pay for event E_j.

• While E_j has not been fully paid for:
  • Among the accounts that are open at time e_j and that have not yet been fully depleted, let A_i be an account with the earliest end date.
  • Deduct from A_i the smaller of the remaining unpaid portion of the event, and the amount of money left in the account.

The intuition of Early is that you should pay from the account that will expire soonest.

Level

Assume that events 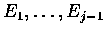$E_1, \ldots, E_{j-1}$ have been paid for, and we now wish to pay for event E_j. Partition the cost of E_j among the open accounts in such a way that the amount of money remaining, in the open account with the most money remaining, is as small as possible.

• If you need to know, this can be accomplished in the following manner (although how this is accomplish is not really germane to the correctness issue at hand): The open account with the largest balance pays for part of E_j until the balance in this biggest open account is equal to the balance in the second biggest open account; Then these two open accounts pay for the remaining portion of cost equally until their balances equals the balance in the third biggest open account; Then these three open accounts pay for the remaining portion of cost equally until $\ldots$.

The intuition of Level is that you should not deplete any account unless it is necessary to do so.

As an example of the algorithms assume that we have two events E₁ and E₂, with e₁ = 5 and e₂=7, and with c₁=60 and c₂=50. So event E₁ can only charged to accounts A_i satisfying $r_i \le 5 \le d_i$, and event E₂ can only charged to accounts A_i satisfying $r_i \le 7 \le d_i$. Assume that accounts A₇ and A₉ have the property that r₇ < r₉ < e₁ = 5 < e₂ = 7 < d₇ < d₉, so accounts A₇ and A₉ can pay for events E₁ and E₂. Assume all other accounts A_i either have d_i < 5 or r_i>7, so they are not eligible to pay for either event E₁ or event E₂. Assume that the initial balance in A₇ is a₇=$100, and that the initial balance in A₉ is a₉=$80.

First Early will charge all of the cost of $60 for E₁ to A₇ since d₇ < d₉. Then Early will charge the first $40 for E₂ to A₇ since d₇ < d₉. But at that time A₇ will be depleted, and then Early will charge the last $10 of the cost of E₂ to A₉.

First Level will charge $40 of the cost of E₁ to A₇ and $20 of the cost of E₁ to A₉, leaving both account balances at $60. The $50 cost of E₂ will be split evenly by A₇ and A₉, that is, each of these account pays $25, leaving the account balance of each account at $35.

For each of the algorithms Early and Level, prove or disprove that the algorithm correctly solves this problem

2.

(20 points) We consider the problem of computing the shortest common super-sequence of two sequences $A=a_1, \ldots, a_m$ and $B=b_1, \ldots, b_n$. Let T(i,j) be the length of the shortest common super-sequence of $a_1, \ldots, a_i$ and $b_1, \ldots, b_j$.

(a)

Write a recursive function in C like pseudo-code to compute T(i, j) in the naive way. Don't forget the base case(s).

(b)

Explain as precisely as you can why the running time of your function would be exponential in n and/or m for some inputs.

(c)

Write iterative array-based pseudo-code to compute T(m, n) that runs in 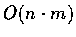$O(n \cdot m)$ time.

(d)

Write pseudo-code to actually find the shortest common super-sequence from your array.

3.

Consider the following problem. The input is a sequence $x_1, \ldots, x_n$ of integers. The integers may be negative, 0 or positive. The goal is to find an increasing subsequence of maximum sum. That is, find a subsequence $x_{i_1} < \ldots x_{i_k}$ $\sum_{j=1}^k x_{i_j}$ is as large as possible. So for example, if the input was 5, 6, 9, 1, 2, 3, 7, 8, 4, the answer would be 5, 6, 7, 8 since this subsequence is increasing and has sum 26 (and no other increasing subsequence has sum greater than 26).

(a)

(15 points) Give an O(n²) time iterative array-based algorithm to compute the largest weight that is achievable. Note that the sum of the number may be much larger than n², so the size of any array you use can not depend on the size of the numbers. However, you may assume the numbers are small enough to fit within a few words of memory. You should read the next subproblem before attempting this subproblem.

(b)

(5 points) Give an O(n) time algorithm to compute the actual subsequence from the table/array that you constructed in the previous subproblem.

4.

(20 points) Consider the problem where the input is a collection of n train trips within Germany. For the ith trip T_i you are given the date d_i of that trip, and the non-discounted fare of f_i Euros for that trip. The Deutsche Bahn sells a yearly Bahncard for C Euros that entitles you to a 50% fare reduction on all train travel within Germany within Y days of purchase. The Deutsche Bahn also sells a monthly Bahncard for D Euros that entitles you to a 10 Euro fare reduction on all train travel within Germany within M days of purchase. You may have both a monthly and a yearly Bahncard, and the yearly Bahncard discount applies first. Assume for simplicity that the possible dates of travel are just represented by the integers $1, \ldots, k$. So if you have trip scheduled on day d_i with fare f_i, this trip will cost

• f_i Euros if you did not buy a yearly Bahncard since day d_i - Y, and you did not buy a monthly Bahncard since day d_i - M.
• f_i/2 Euros if you did buy a yearly Bahncard since day d_i - Y, and you did not buy a monthly Bahncard since day d_i - M.
• f_i - 10 Euros if you did not buy a yearly Bahncard since day d_i - Y, and you did buy a monthly Bahncard since day d_i - M.
• (f_i/2) - 10 Euros if you did buy a yearly Bahncard since day d_i - Y, and you did buy a monthly Bahncard since day d_i - M.

The problem is to determine the cheapest possible cost to take your trips. You need not actually compute when to buy the various Bahncards. Give an O(n³) time algorithm for this problem.