CS 1510 Midterm 1

Fall 2000

1.

(40 points) We consider the following problem:

INPUT: A collection of jobs $J_1, \ldots, J_n$, where the ith job is a 3-tuple (r_i, x_i, d_i) of non-negative integers.

OUTPUT: 1 if there is a preemptive feasible schedule for these jobs on one processor, and 0 otherwise. A schedule is feasible if every job job J_i is run for x_i time units between its release time r_i and its deadline d_i.

We consider greedy algorithms for solving this problem that schedule times in an online fashion, that is the algorithms are of the following form:

t = 0;

while there are jobs left not completely scheduled

        pick a job J_m to schedule at time t;

        increment t;

One can get different greedy algorithms depending on how job J_m is selected. For each of the following method of selecting J_m, prove or disprove the that resulting greedy algorithms produce feasible schedules, if they exist for the jobs being considered.

(a)

Among those jobs J_i such that 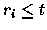$r_i \le t$, and that have not been scheduled for enough time units, pick J_m to be the job with minimal deadline. Ties may be broken arbitrarily. We call this algorithm EDF.

(b)

Among those jobs such that 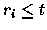$r_i \le t$, and that have not been scheduled for enough time units, pick J_m to be the job that has minimal remaining processing time. Ties may be broken arbitrarily. If a job have been executed for y time units before time t, then its remaining processing time is x_i -y. We call this algorithm SRPT.

As an example of EDF and SRPT consider the following instance: J₁=(0, 100, 1000), J₂=(10, 10, 100), J₃=(10, 10, 101), and J₃=(115, 10, 130).

EDF runs J₁ from time 0 through time 10. From time 10 until time 20, EDF runs J₂ because J₂'s deadline, 100, is less than J₁'s deadline, 1000, and less than J₃'s deadline, 101. From time 20 until time 30, EDF runs J₃ because J₃'s deadline, 101, is less than J₁'s deadline, 1000, From time 30 to time 115, EDF runs J₁. From time 115 to time 125, EDF runs J₄ since J₄'s deadline, 130, is less than J₁'s deadline, 1000. EDF then runs J₁ from time 125 to time 130. Thus for this input, EDF finishes all the jobs by their deadline.

SRPT runs J₁ from time 0 through time 10. From time 10 until time 30, SRPT runs J₂ and J₃ (either can go first) because through out this time period, J₂ and J₃'s remaining processing times are always equal and less than J₁'s remaining processing time, 90. From time 30 to time 115, SRPT runs J₁. From time 115 to time 120, SRPT runs J₁ since J₁'s remaining processing time throughout this period is smaller than J₄'s remaining processing time, 10. From time 120 to 130, SRPT runs J₄. Thus for this input, SRPT finishes all the jobs by their deadline.

2.

(20 points) Consider the following problem of computing the optimal binary search tree that we covered in class, and that is covered in the text:

INPUT: Probabilities $p_1, \ldots, p_m$

OUTPUT: The minimum expected depth of a binary search tree with n keys, $K_1 < \ldots < K_n$, given that K_i is accessed with probability p_i.

Recall that the expected depth of a key is given by the formula

$$\sum_{i=1}^n p_i \cdot {\rm depth}(K_i)$$

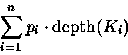
Note that we are only interested in computing the expected depth, not the actual tree. Assume that the depth of the root is 1. Let MIN(i, j), $1 \le i \le j \le n$ be the minimum expected depth for keys K_i through K_j.

(a)

Give a recurrence relation for MIN(i,j).

(b)

Give convincing evidence that if the recurrence was implemented in C in a naive recursive manner that the running time of the resulting algorithm would be exponential in n.

(c)

Now consider MIN as an array. Give iterative array-based pseudo-code to fill-in the entries in MIN.

(d)

Use this code to compute the remaining entry in the following table when p₁=.4, p₂=.3, p₃=.1 and p₄=.2. Show your calculations. Assume the pre-computed entries are correct.

	j=1	j=2	j=3	j=4
i=1	.4	1	2
i=2	UNDEFINED	.3	.5	1.5
i=3	UNDEFINED	UNDEFINED	.1	.4
i=4	UNDEFINED	UNDEFINED	UNDEFINED	.2

3.

(20 points) Give an algorithm for the following problem whose running time is bounded by a polynomial in n+L.

INPUT: A set positive integers $X= \{x_1, \ldots, x_n\}$, and a positive integer K.

OUTPUT: 1 if there exists a subset S of X, and 0/1 variables $y_1, \ldots, y_n$ such that

$$\sum_{x_i \in S} (-1)^{y_i} x_i = K$$

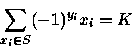
and 0 otherwise.

Here $L= \sum_{i=1}^n x_i$ is the sum of all the x_i. So in words, you have three mutually exclusive choices for each number x_i:

• You can not include x_i in the sum, or
• you can include x_i in the sum positively, or
• you can include x_i in the sum negatively.

So if the input was $X = \{ 2, 6, 7, 9, 11, 14\}$ and K= 8, you algorithm should output 1, since one could take $S = \{ 2, 7, 11, 14 \}$, y₁=1, y₃=0, y₅=1 and y₆=0, and get -2 + 7 - 11 + 14 = 8.

4.

(20 points) Give an algorithm for this problem whose running time is bounded by a polynomial in n.

INPUT: Intervals $(a_1, b_1), \ldots (a_n, b_n)$ over the real line and a positive integer L such that for all i, $1 \le i \le n$, it is the case that 0 < a_i < b_i < L. That is, all intervals start after time 0 and end before time L. Think as each interval (a_i, b_i) as being a request for a room from time a_i to time b_i.

OUTPUT: A non-intersecting sub-collection S of the intervals that minimizes the maximum contiguous time that the room is empty between time 0 and time L. That is, assume that

$$S = \{ (a_{i_1}, b_{i_1}), \ldots, (a_{i_k}, b_{i_k}) \}$$

with

$$0 < a_{i_1} < b_{i_1} < a_{i_2} < b_{i_2} < \ldots < a_{i_k} < b_{i_k} < L$$

Then the maximum contiguous time that the room is empty is

$$\max [ a_{i_1} - 0, L - b_{i_k}, \max_{1 \le j \le k-1} (b_{i_{j+1}} - a_{i_j})]$$

As an example, consider the input $\{ (2, 5), (3, 9), (7, 10), (2, 11), (15, 20), (18, 49), (34, 44) \}$ and L=50. One feasible solution would be $S =\{ (2, 5), (7, 10), (15, 20), (34, 44) \}$. For this S, the room would be empty during the following time intervals (0, 2), (5, 7), (10, 15), (20, 34), (44, 50). Thus the longest time the room will be empty is the 14 time units between time 20 and time 34. There is no claim that this S is the optimal S for this input.